Education | Ultimate Fixed Income 101: What is Duration?

Hi All,

We will discuss 'duration' today which is a key risk measure when looking at bonds. As I write this, the yield curve's inversion is at its deepest in decades, this makes duration management more important along with the yield curve moves in one's portfolio.  

I will look to share more in-depth calculation examples in the future.

Today's Key Concepts

1. What is Duration?
2. Types of Duration
3. What is Convexity?
4. Limitations of Duration

☘️1. What is Duration?

Duration is a measure of a bond's sensitivity to changes in interest rates. It is a way of estimating how much a bond's price will change in response to changes in interest rates. Typically, duration is expressed in years, and it takes into account the bond's maturity, coupon rate, and yield to maturity.

*History of Duration:

The concept of duration was first introduced by economist Frederick Macaulay in 1938 to determine the price volatility of bonds. Today, the most commonly used duration measure is "Macaulay duration." However, prior to the 1970s, duration was not widely utilized due to the relatively stable interest rates. It wasn't until interest rates experienced a significant increase that investors began to take notice of duration as a valuable tool for assessing the price volatility of their fixed income investments. During this time, "modified duration" was developed, providing a more precise calculation of bond price changes based on different coupon payment schedules. Later in the mid-1980s, as interest rates started to decline, investment banks created the concept of "option-adjusted duration" or "effective duration," which allowed for the calculation of price movements while taking into account call features.

*Importance of Duration in Bond Investing:

Duration is arguably one of the most important concepts in bond investing, as it helps investors understand the risk and potential return of a bond.

Duration is a useful tool for estimating the potential change in a bond's price in response to fluctuations in interest rates. In general, for every year of duration, a bond's price is expected to move approximately 1% in the opposite direction of the change in interest rates. For instance, if a bond has a duration of 3 years and interest rates increase by 1%, the bond's price is expected to decrease by around 3%. Conversely, if interest rates decrease by 1%, the bond's price is expected to rise by about 3%.

In simple terms, another way to understand the concept of duration is to see it as the average time it takes to receive all the cash flows of a bond, weighted by the present value of each of the cash flows. In essence, it represents the point in time at which an investor can expect to recover their initial investment.

As such, duration enables the effective comparison of bonds with varying maturities and coupon rates by providing a relative measure of their ability to predict price changes based on interest rate fluctuations. For instance, a 5-year zero coupon bond may exhibit greater sensitivity to interest rate changes compared to a 7-year bond with a 6% coupon.

*Interesting Facts about Duration

• Longer the maturity, the longer the duration because it takes more time to receive full payment. The shorter a bond’s maturity, the shorter its duration, because it takes less time to receive full payment.
• Higher the coupon rate, the shorter the duration. This is because more coupon payment is received before final maturity. As such, the lower a bond’s coupon, the higher its duration, because proportionately more payment is received before final maturity.
• Higher the YTM, the shorter the duration.
• For a zero coupon bond, Bond's maturity = duration.
• Bonds with longer durations are generally more sensitive to changes in interest rates, and may be riskier than bonds with shorter durations. By understanding the duration of a bond, investors can make more informed investment decisions and manage their portfolio risk.

*Relationship between Duration and Interest Rates:

The relationship between duration and interest rates is inverse. When interest rates rise, bond prices fall, and when interest rates fall, bond prices rise. The magnitude of the change in bond prices is directly related to the bond's duration. Bonds with longer durations will experience greater price changes in response to changes in interest rates, while bonds with shorter durations will experience smaller price changes.

☘️ 2. Types of Duration

Hope I haven't lost you yet. It can get confusing but hopefully laying out different types of duration calculations can further clarify the concept. There are five different types of duration you will hear about when we talk about fixed income investing.

1. Maucaley Duration: estimates how many years it will take for an investor to be repaid the bond’s price by its total cash flows. Investopedia has more info.

2. Modified Duration: measures the price change in a bond given a 1% change in interest rates. Investopedia has more info.

3. Dollar Duration (DV01): This is a widely used concept among fixed-income portfolio managers. The dollar duration measures the change in the value of a bond portfolio for every 100 basis point (1%) change in interest rates.

Note) it is based on a linear approximation of how a bond's value will change in response to changes in interest rates. However, the actual relationship between a bond's value and interest rates is not linear. Therefore, dollar duration is an imperfect measure of interest rate sensitivity, and it will only provide an accurate calculation for small changes in interest rates. Investopedia has more.

4. Key Rate Duration: This is another widely used concept among fixed-income portfolio managers esp. for sovereign bonds. The key rate duration calculates the change in a bond's price in relation to a 100-basis-point (1%) change in the yield for a given maturity.

Note) When a yield curve has a parallel shift, you can use effective duration, but key rate duration must be used when the yield curve moves in a non-parallel manner, to estimate portfolio value changes. Investopedia has more.

5. Effective Duration: Effective duration is used to calculate the duration for bonds with embedded options. It calculates the expected price decline of a bond when interest rates rise by 1%. Investopedia has more.

☘️ 3. What is Convexity?

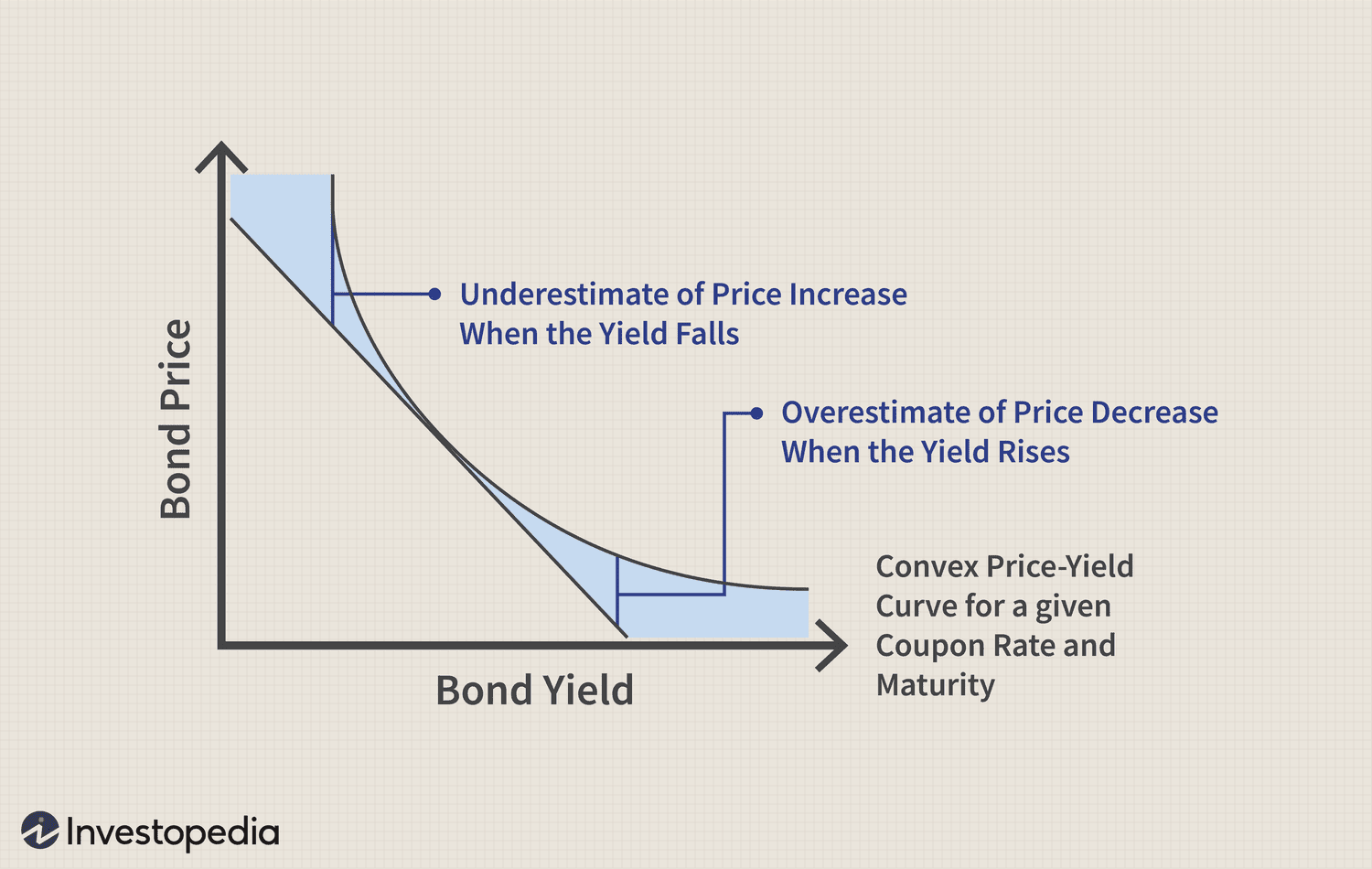
Duration assumes a linear relationship between bond prices and changes in interest rates.

However, in reality, as interest rates increase, bond prices tend to go down less, while the prices tend to go up more when interest rates decrease. This disparity implies that duration tends to overestimate the amount of price decline associated with a significant upward move in interest rates. Conversely, duration tends to underestimate the amount of price increase associated with a substantial drop in interest rates.

To address this disparity, the concept of "convexity" was introduced. Convexity accounts for the error produced by duration in predicting price changes in response to significant movements in interest rates. By measuring the rate of change in duration, convexity fully captures the dynamic relationship between bond prices and interest rates.

Convexity can aid in predicting the speed at which bond prices are expected to change in response to interest rate fluctuations. Holding all other factors constant, higher convexity may make bonds more appealing since it can lead to greater price appreciation when interest rates fall and smaller price declines when interest rates rise. Investopedia has more info.

☘️ 4. Limitations of Duration

While duration is a useful measure of bond risk, it does have some limitations. For example:

• Duration is based on a number of assumptions about interest rate changes, and these assumptions may not always hold true in the real world.
• Duration assumes that all interest rate changes are parallel, meaning that all bonds will move by the same amount in response to a given change in interest rates. However, this is not always the case, and some bonds may be more or less sensitive to interest rate changes than others.
• Duration is less accurate for bonds with complex cash flows, such as mortgage-backed securities or callable bonds, where the timing and size of future cash flows can be difficult to predict. This is where the concept of 'convexity' comes into play.

Despite these limitations, duration remains a widely used measure of bond risk, and is an important tool for bond investors.